贝塞尔曲线
贝塞尔曲线
贝塞尔曲线(读作 [bezje])是一种使用数学方法描述的曲线,被广泛用于计算机图形学和动画中。在矢量图中,贝塞尔曲线用于定义可无限放大的光滑曲线。
贝塞尔曲线由至少两个控制点进行描述。Web 技术中使用的是三次贝塞尔曲线,即使用四个控制点 P0、P1、P2 和 P3 描述的曲线。
在绘制二次贝塞尔曲线的过程中,需要先作两条辅助线:P0 到 P1 和 P1 到 P2;第三条辅助线从其起点稳步移动到第一辅助线上,终点在第二辅助线上。在这条辅助线上,有一个点从其起点稳步移动到其终点。这个点描述的曲线就是贝塞尔曲线。以下是一个动画示例,展示了曲线的创建过程:
![二次贝塞尔曲线演示动画,t in [0,1]](./贝塞尔曲线/Bézier_2_big-1763785403485-3.gif)
一般化
术语
一些关于参数曲线的术语,有
又称作n阶的伯恩斯坦基底多项式,定义
点
构建贝塞尔曲线
线性曲线
线性贝塞尔曲线函数中的t会经过由
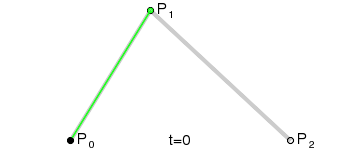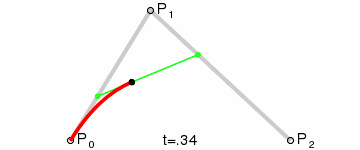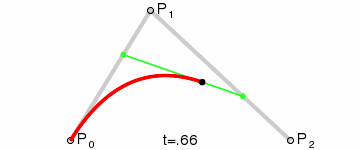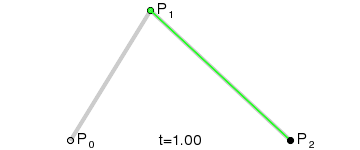
二次曲线
为建构二次贝塞尔曲线,可以中介点Q0 和Q1 作为由 0 至 1 的t:
- 由P0 至P1 的连续点Q0,描述一条线性贝塞尔曲线。
- 由P1 至P2 的连续点Q1,描述一条线性贝塞尔曲线。
- 由Q0 至Q1 的连续点B(t),描述一条二次贝塞尔曲线。
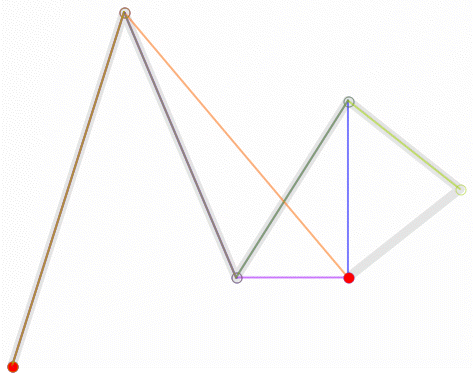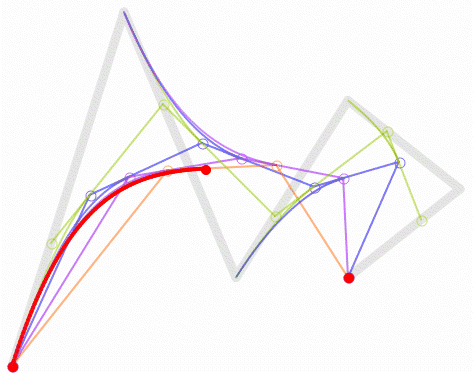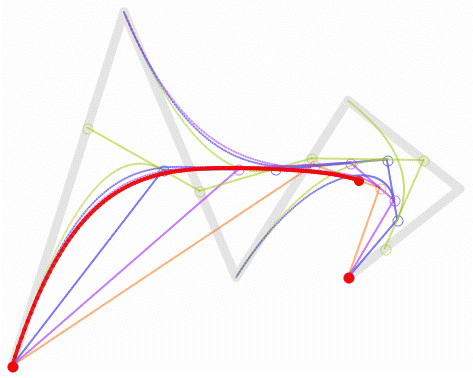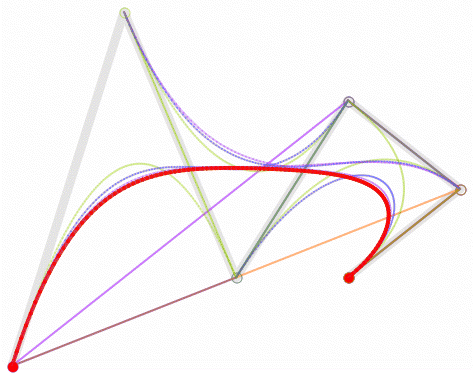
高阶曲线
为建构高阶曲线,便需要相应更多的中介点。对于三次曲线,可由线性贝塞尔曲线描述的中介点Q0、Q1、Q2,和由二次曲线描述的点R0、R1 所建构:
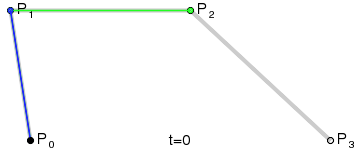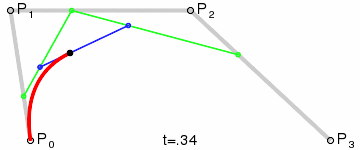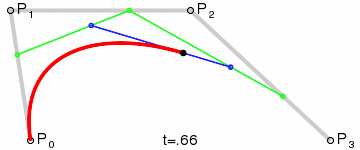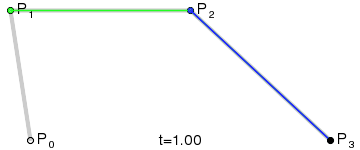
对于四次曲线,可由线性贝塞尔曲线描述的中介点Q0、Q1、Q2、Q3,由二次贝塞尔曲线描述的点R0、R1、R2,和由三次贝塞尔曲线描述的点S0、S1 所建构:
升阶
n次贝塞尔曲线可以变换为一个形状完全相同的n+1次贝塞尔曲线。 这在软件只支持特定阶次的贝塞尔曲线时很有用。 例如,Cairo只支持三次贝塞尔曲线,你就可以用升阶的方法在 Cairo 画出二次贝塞尔曲线。
我们利用
对任何的n值,我们都可以使用以下等式
式中
因此,新的控制点为
- Title: 贝塞尔曲线
- Author: Ryan Lu
- Created at : 2024-09-19 22:16:03
- Updated at : 2026-02-05 03:31:06
- Link: http://ryan-hub.site/a0265d14976c/
- License: This work is licensed under CC BY-NC-SA 4.0.